3. Поиск решения

Задачи, выполняемые с использованием процедуры поиска решения, относятся к сравнительно узкой области. Такие задачи называют оптимизационными. Обычно они затрагивают случаи, удовлетворяющие следующим условиям.

1. Значение в целевой ячейке зависит от других ячеек и формул. Нужно определить все исходные параметры, при которых значение в целевой ячейке будет максимальным, минимальным или заранее определенным;

2. Целевая ячейка зависит от группы ячеек, которые называются изменяемыми ячейками. Их значения надо подобрать так, чтобы получить желаемый результат в целевой ячейке.

3. Решение (значения изменяемых ячеек) должно находиться в определенных пределах или удовлетворять определенным ограничениям.

После соответствующей подготовки рабочего листа можно использовать процедуру поиска решения для подбора значений в изменяемых ячейках и получения в целевой ячейке нужного результата, который одновременно удовлетворяет все установленным ограничениям.

Установка расширения.

Пакет Поиск решения не входит в стандартную поставку OpenOffice.org Calc, поэтому если он ещё не установлен то необходимо его установить.

1. Расширение Поиск решения находится в каталоге с лабораторными работами. Если его там нет то можно скачать его с сайта (http://kohei.us/ooo/solver). Скачайте оттуда последнюю версию расширения (файл scsolver.uno.oxt) в каталог Расширения внутри каталога с лабораторной работой, а если его нет, то создайте.

2. Выполните команду Сервис⇒Управление расширениями и в появившемся окне нажмите кнопку Добавить рис.5

Рис 5.

3. В диалоге выбора файла в каталоге Расширения выберите файл scsolver.uno.oxt и нажмите Открыть Рис. 6.

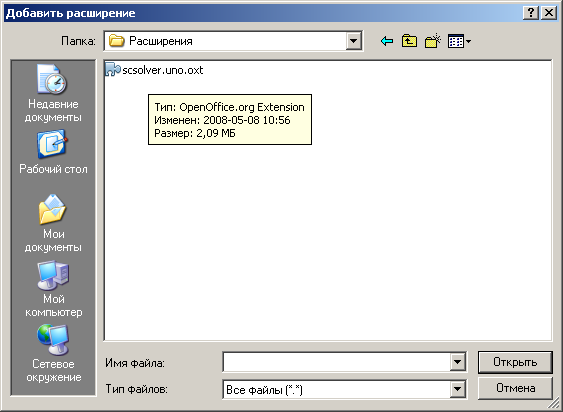
Рис 6

4. В открывшемся диалоге лицензионного соглашения нажимайте кнопку Листать для пролистывания лицензии, до тех пор пока не станет активна кнопка Принять рис. 7.

5. Нажмите на кнопку принять.

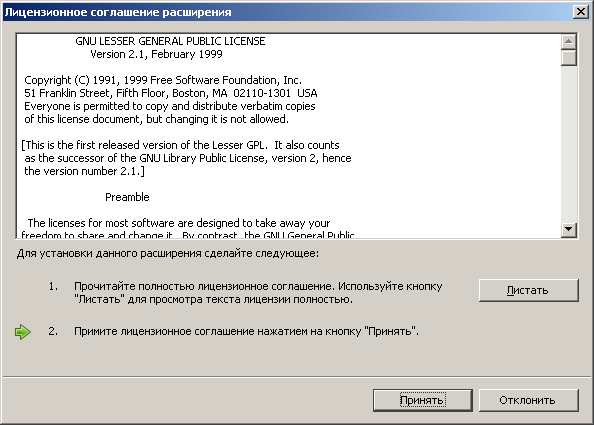
Рис. 7.

6. После установки проверьте наличие расширения в списке Мои расширения рис. 8. рис.9.

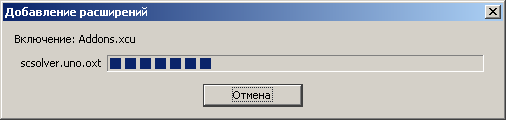
Рис. 8.

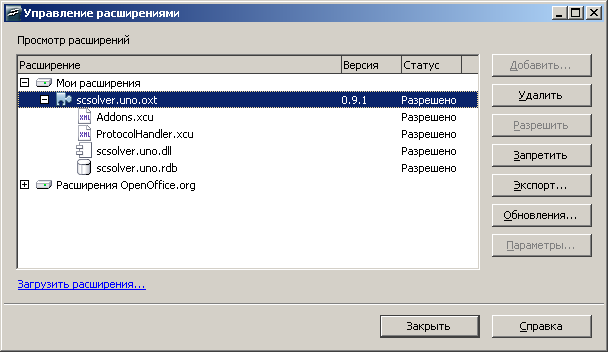
Рис. 9.

7. Закройте диалог нажатием кнопки Закрыть.

8. Перезапустите программу OpenOffice.org Calc.

Решим следующую задачу:

Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м² досок, для изделия модели В – 4 м². Фирма может получать от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, для изделия модели В – 30 мин. В неделю можно использовать 160 ч машинного времени.

Сколько изделий какой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 доллара прибыли, каждое изделие В – 4 доллара прибыли?

Задание:

1. Откройте лист Поиск решения. При отсутствии исходного файла Лист2 назовите Поиск решения, создайте таблицу Таблица 1. Левая верхняя ячейка соответствует ячейке А1.

2. Для решения задачи введем две переменные:

• х - количество изделий модели А;
• у - количество изделий модели В.

3. Ячейки, содержащие переменные, будут являться изменяемыми, т.к. от них будет за­висеть результат в целевой ячейке. Присвойте ячейкам В2 и В3 соответственно имена Х и Y. Для этого активизируйте ячейку В2 и выполните команду Вставка^Названия^Определить В поле Название введите имя ячейки В2 - Х. Нажмите кнопку Добавить. Аналогичным способом присвойте ячейке В3 имя Y, после чего нажмите ОК. Рис.10

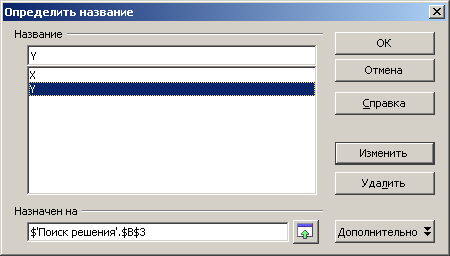
Рис 10

4. Исходя из условия задачи, наша цель - максимизировать прибыль, поэтому целевой функцией будет являться выражение типа: 2х+4у. В ячейку В6 введите формулу для вычисления прибыли рис. 11.

5. Беспредельному увеличению количество изделий препятствуют ограничения, описан­ные в условии задачи:

   • ограничение количества материала для полок в неделю: 3*х+4*у<1700;

   • ограничение количества машинного времени в неделю:

(12/60)*х+(30/60)*у<160 =^> 0,2*х+0,5*у<160.

6. Введите формулы ограничений в ячейки В9 (=3*х+4*у) и В10 (=0,2*х+0,5*у).

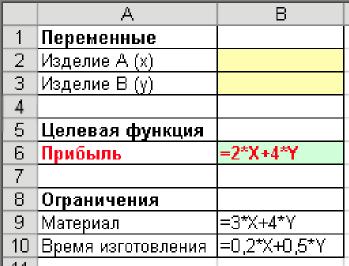
Рис. 11

7. Кроме того, необходимо помнить, что количество изделий – неотрицательное число, поэтому к ранее описанным ограничениям добавляются еще два: х≥0 и у≥0.

8. Количества изделий должны быть целыми числами: х-целое и у-целое.

9. Установите курсор в ячейку целевой функции В6.

10. Выполните команду Сервис⇒Поиск решения.

11. В окне Поиск решения проверьте, чтобы в поле Целевая функция стояла ссылка на ячейку с целевой функцией рис. 12.

12. В поле Цель установите переключатель максимум.

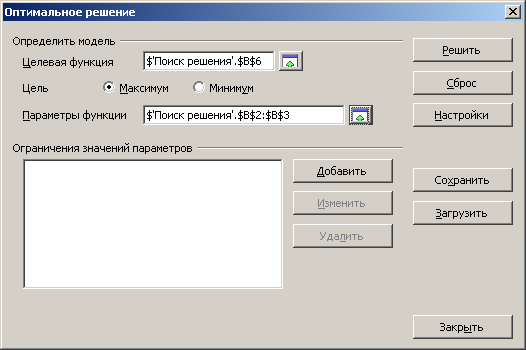
Рис. 12

13. В поле Параметры функции укажите диапазон изменяемых ячеек рис. 131.

14. В поле Ограничения значений параметров задайте ограничения. Для этого нажмите кнопку Добавить, расположенную рядом с данным полем.

15. В появившемся диалоговом окне Добавление ограничения в поле Ссылка на ячейку укажите на ячейку с функцией ограничения материала, в следующем поле из списка выберите оператор ≤ и в поле Ограничение введите число 1700 рис. 13. Нажмите кнопку ОК.

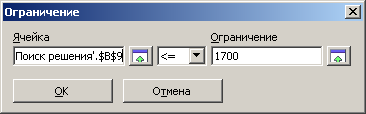
Рис. 13

16. Таким же образом введите оставшиеся три ограничения и нажмите кнопку ОК.

17. Проверьте правильность ввода данных в окне Поиск решения рис. 14 и нажмите кнопку Решить.

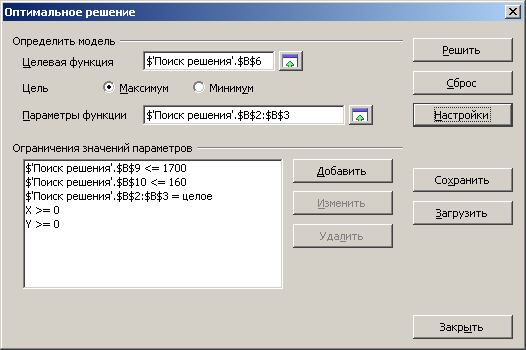
Рис. 14

18. В появившемся окне Решение найдено нажмите ОК после чего закройте окно Оптимальное решение.

19. В изменяемых ячейках появятся значения, являющиеся оптимальными для поставленных условий, в ячейке с целевой функцией отобразится наибольшее значение прибыли рис. 15.

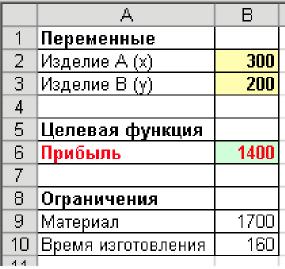
Рис. 15

20. Сохраните файл.