1. Анализ инвестиций

Многие функции для анализа инвестиций имеют одинаковые аргументы. Эти аргументы представлены в таблице 1.

Таблица 1

Аргумент	Название	Описание
Пс	Приведенная стоимость (начальная)	Общая сумма, которая на настоящий момент равноценна ряду будущих выплат
Бс	Будущая стоимость инвестиции	Сумма, которая будет достигнута после последней выплаты
Плт	Выплата	Сумма, выплачиваемая в каждый период и не меняющаяся за все время выплаты инвестиции
Кпер	Общее число периодов выплаты инвестиции	Рассчитывается как произведение количества лет инвестиции на количество выплат в год. Например, кредит выдан на 5 лет с выплатой 2 раза в год. Число периодов равно 5*2=10.
Ставка	Процентная ставка за период	Рассчитывается как процентная ставка за год, деленная на количество выплат в год. Например, кредит выдан под 10% годовых с ежеквартальными выплатами. Процентная ставка за период равна 10/4=2,5%
Тип	Вид аннуитета (тип)	Принимает логическое значение 0 или 1. Значение 0 обозначает, что выплата производится в конце периода, 1 – в начале периода.

Финансовые функции связаны с интервалами выплат. Аннуитет — это ряд постоянных денежных выплат, делаемых в течение длительного периода. Например, заем под автомобиль или заклад являются аннуитетами.

В функциях, связанных с аннуитетами, выплачиваемые денежные средства, такие как депозит на сбережения, представляются отрицательным числом; полученные денежные средства, такие как чеки на дивиденды, представляются положительным числом.

Например, депозит в банк на сумму 1000 руб. представляется аргументом -1000 — для вкладчика и аргументом 1000 — для банка.

1.1. Расчет текущей стоимости инвестиции. Функция PV (ПС)

Функция PV (приведенная стоимость) является одним из наиболее распространенных способов оценки привлекательности долговременных вложений. Текущее значение вложения (чистый текущий объем вклада) определяется дисконтированием (приведением к стоимости на настоящий момент) поступлений по этому вложению. Если текущая стоимость поступлений оказывается больше вклада, вложение считается удачным.

Синтаксис функции: PV(Ставка;Кпер;Плт; Бс; Тип)

Функция PV вычисляет текущую стоимость ряда равных по величине периодических выплат или единовременной выплаты.

Для вычисления текущей стоимости ряда выплат используется аргумент Плт (выплата).

Для вычисления текущей стоимости единовременной выплаты используется аргумент Бс (будущая стоимость).

Для вложения с рядом периодических выплат и единовременной выплаты используются оба эти аргумента.

Задача 1. Определение текущей стоимости ряда периодических выплат.

Существует два варианта вложения денежных средств с целью заработать 5 000р. в течение 2,5 лет:

1. Совершить сделку, которая каждые полгода возвращает 1 000р. в течение следующих 2,5 лет. Для этого нужно вложить 4 000р.

2. Вложить деньги в банк на краткосрочный счет под 8,0% с выплатами каждые полгода в размере 1 000р.

Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче.

Решение этой задачи требует оценить текущую стоимость ряда поступлений по 1 000р. Проценты, которые предлагает банк, послужат в качестве учетной ставки вложения. Учетная ставка является своего рода «барьером», который должен быть превзойден, прежде чем инвестиция станет привлекательной, поэтому ее часто называют барьерной ставкой.

Для определения текущей стоимости вложения используется функция PV, в которой будет задействован аргумент Плт и не задействован аргумент Бс.

Ход решения задачи.

1. Из папки Материалы откройте файл Лаб.раб.6. При отсутствии папки Материалы создайте новую рабочую книгу OpenOffice.org Calc и назовите ее Лаб.раб.6.
2. Активизируете лист ПС. При отсутствии исходного файла Лист1 назовите ПС и создайте таблицу согласно таблице 2.

3. Вычислите количество периодов выплат и ставку за период см. табл.1.

4. Используя Мастер функций, ознакомьтесь с функцией PV (ПС).

5. Вычислите текущую стоимость инвестиции. Результаты сравните с рисунком рис. 1.

Рис. 1

6. Сохраните файл.

Анализ результатов решения.

Функция возвращает значение -4 451,82. Это означает, что нужно вложить в банк 4 451,82р. под 8,0% годовых сегодня, чтобы получить 5 000р. в течение следующих 5 лет. Поскольку в предлагаемой сделке вклад равен 4 000р., можно считать, что совершить сделку выгоднее, чем вложить деньги в банк.

Задача 2. Определение текущей стоимости единовременной выплаты.

Существует два варианта вложения денежных средств с целью получения 5 000р. по истечению 2,5 лет:

1. Совершить сделку, вложив 4 000р.

2. Вложить деньги в банк на краткосрочный счет под 8,0% с начислением процентов каждые полгода.

Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче.

Решение этой задачи требует оценить текущую стоимость единовременной выплаты. Для определения текущей стоимости вложения используется функция PV, в которой будет задействован аргумент Бс и не задействован аргумент Плт.

Ход решения задачи.

1. При отсутствии исходного файла на листе PV создайте таблицу согласно таблице 3.

2. Вычислите количество периодов выплат и ставку за период см. табл.29.

3. Вычислите текущую стоимость инвестиции. Результаты сравните с рисунком рис.2.

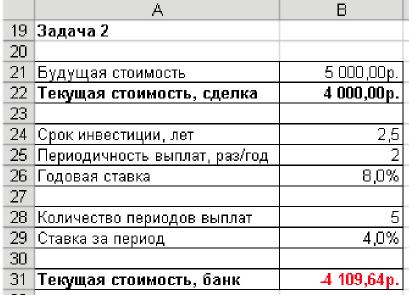
Рис. 2

4. Сохраните файл.

Анализ результатов решения.

Функция возвращает значение -4 109,64. Это означает, что нужно вложить в банк 4 109,64р. под 8,0% годовых сегодня, чтобы получить 5 000р. через 5 лет. Поскольку значение 4 109,64р. больше, чем текущая стоимость сделки (4 000р.), вложить деньги в сделку более выгодно, чем в банк.

Задача 3. Определение текущей стоимости ряда платежей и единовременной выплаты.

Существует два варианта вложения денежных средств сроком на 2,5 года.

1. Совершить сделку, которая ежегодно возвращает 500р. в течение следующих 2,5 лет. Кроме того, в конце периода будет выплачено 3 000р.

2. Вложить деньги в банк на краткосрочный счет под 8,0% с начислением процентов каждые полгода.

3. Определить, какой из вариантов вложения денежных средств является более выгодным.

Пояснения к задаче.

Решение этой задачи требует оценить текущую стоимость ряда платежей и единовременной выплаты. Для определения текущей стоимости вложения используется функция PV, в которой будут одновременно задействованы аргументы Бс и Плт.

Ход решения задачи.

1. При отсутствии исходного файла на листе PV создайте таблицу согласно таблице 4.

Таблица 4

Будущая стоимость	3 000,00р.
Текущая стоимость, сделка	4 000,00р.
Выплата за период	500,00р.
Срок инвестиции, лет	2,5
Периодичность выплат, раз/год	2
Годовая ставка	8,00%
Количество периодов выплат
Ставка за период
Текущая стоимость, банк

2. Вычислите количество периодов выплат и ставку за период см. табл.1.

3. Вычислите текущую стоимость инвестиции. Результаты сравните с рисунком.

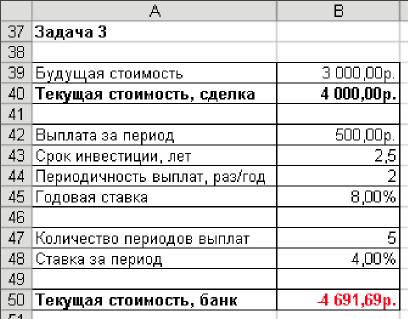
Рис. 3

4. Сохраните файл.

Анализ результатов решения.

Функция возвращает значение -4 691,69. Это означает, что нужно вложить в банк 4 691,69р. под 8,0% годовых. Поскольку значение 4 691,69р. больше, чем текущая стоимость сделки (4 000р.), вложить деньги в сделку более выгодно, чем в банк.

Задача 4. Определение наиболее выгодного варианта вложения денежных средств.

Существует несколько вариантов вложения денежных средств в размере 45 000р. с целью получения 70 000р. в течение 7 лет. Предполагается, что выплаты будут производиться 2 раза в год.

Определите, что выгоднее: вложить деньги в банк на краткосрочный счет под 12% или совершить одну из нижеуказанных сделок?

1. Сделка, которая каждые полгода возвращает 5 000р. Для этого нужно вложить 45 000р.

2. Сделка, в которую надо вложить 45 000р. для получения единовременной выплаты в размере 70 000р.

3. Сделка, которая каждые полгода возвращает 2 500р. в течение следующих 7 лет. Кроме того, в конце периода будет выплачено 40 000р.

Пояснения к задаче.

Решение этой задачи требует оценить текущую стоимость вложения в банк по условиям указанных сделок и сравнить полученные значения с текущей стоимостью сделок. На основании сравнения необходимо сделать выводы о выгодности вложений.

Ход решения задачи.

1. При отсутствии исходного файла на листе PV создайте таблицы согласно таблицам 5-7.

Таблица 5

Вариант 1
Текущая стоимость, сделка	45 000,00р.
Выплата за период	5 000,00р.
Срок инвестиции, лет	7
Периодичность выплат, раз/год	2
Годовая ставка	12,00%
Количество периодов выплат
Ставка за период
Текущая стоимость, банк

Таблица 6

Вариант 2
Будущая стоимость	70 000,00р.
Текущая стоимость, сделка	45 000,00р.
Срок инвестиции, лет	7
Периодичность выплат, раз/год	2
Годовая ставка	12,00%
Количество периодов выплат
Ставка за период
Текущая стоимость, банк

Таблица 7

Вариант 3
Будущая стоимость	40 000,00р.
Текущая стоимость, сделка	45 000,00р.
Выплата за период	2 500,00р.
Срок инвестиции, лет	7
Периодичность выплат, раз/год	2
Годовая ставка	12,00%
Количество периодов выплат
Ставка за период
Текущая стоимость, банк

2. Для каждого из вариантов вычислите текущую стоимость инвестиции.

3. Проанализируйте полученные значения, определите наиболее выгодный вариант вложения.

4. Сохраните файл.

1.2. Расчет будущей стоимости инвестиции. Функция FV (БС)

Функция БС (будущая стоимость) вычисляет для некоторого будущего момента времени величину вложения, которая образуется в результате единовременной выплаты или/и ряда постоянных периодических платежей.

Синтаксис функции: FV (Ставка; Кпер; Плт; Пс; Тип).

Для определения будущего значения ряда выплат используется аргумент Плт (выплата), аргумент Пс (приведенная стоимость) служит для определения будущего значения единовременной выплаты.

Задача 5. Определение наиболее выгодного варианта вложения денежных средств.

Вкладчик планирует открыть счет сроком на 5 лет с ежемесячными платежами и рассчитывает на среднюю скорость оборота 11% в год. Выплаты производятся в начале периода. Существует несколько вариантов вложения:

1. Вносить на счет 2 000р. каждый месяц в течение 5 лет.

2. Вложить 100 000р. с целью получения по истечении 5 лет единовременной выплаты.

3. Внести на счет 30 000р. и далее вносить на счет 1 500р. каждый месяц в течение 5 лет.

Определите наиболее выгодный вариант вложения денежных средств.

Пояснения к задаче.

Решение этой задачи требует оценить текущую стоимость вложения в банк по условиям указанных сделок и сравнить полученные значения с текущей стоимостью сделок. На основании сравнения необходимо сделать выводы о выгодности вложений.

Для определения текущей стоимости вложения используется функция БС. Аргументу Тип задано значение 1 (вложения производятся в начале каждого периода).

Ход решения задачи.

1. Активизируете лист ПС. При отсутствии исходного файла Лист2 назовите FV и создайте таблицы согласно таблицам 8-10.

Таблица 8

Вариант 1
Выплата за период	-2 000,00р.
Срок инвестиции, лет	5
Периодичность выплат, раз/год	12
Годовая ставка	11,00%
Количество периодов выплат
Ставка за период
Будущая стоимость, банк

Таблица 9

Вариант 2
Текущая стоимость	-100 000,00р.
Срок инвестиции, лет	5
Периодичность выплат, раз/год	12
Годовая ставка	11,00%
Количество периодов выплат
Ставка за период
Будущая стоимость, банк

Таблица 10

Вариант 3
Текущая стоимость	-30 000,00р.
Выплата за период	-1 500,00р.
Срок инвестиции, лет	5
Периодичность выплат, раз/год	12
Годовая ставка	11,00%
Количество периодов выплат
Ставка за период
Будущая стоимость, банк

2. Для каждого из вариантов вычислите будущую стоимость инвестиции.

3. Проанализируйте полученные значения, определите наиболее выгодный вариант вложения.

4. Сохраните файл.

1.3. Расчет периодического платежа. Функция PMT(ПЛТ)

Функция PMT вычисляет размер периодической выплаты, необходимой для погашения ссуды за указанное число периодов.

Синтаксис функции: PMT(Ставка; Кпер; Пс; Бс; Тип).

Задача 6. Определение величины периодического платежа.

Взята ссуда размером 50 000р. на срок 2 года под 6% годовых с ежеквартальной выплатой платежей. Необходимо определить величину периодического платежа.

Ход решения задачи.

1. Активизируете лист ПЛТ. При отсутствии исходного файла Лист3 назовите ПЛТ и создайте таблицу согласно таблицам 11.

Таблица 11

Сумма займа	50 000,00р.
Процентная ставка годовая	6,0%
Срок займа в годах	2
Периодичность выплат, раз/год	4
Общее количество выплат
Процентная ставка за квартал
Величина платежа

2. Вычислите количество периодов выплат и ставку за период см. табл.1.

3. Вычислите величину платежа. Результаты сравните с рисунком.

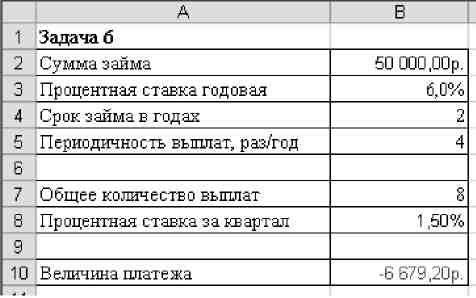
Рис. 4

4. Сохраните файл.

1.4. Составление графика погашения займа.

Функции IPMT (ПРПЛТ), PPMT (ОСПЛТ)

Функция IPMT вычисляет платежи по процентам за заданный период при постоянных периодических выплатах и постоянной процентной ставке.

Синтаксис функции: IPMT(Ставка; Период; Кпер; Пс; Бс; Тип).

Функция PPMT вычисляет основные платежи за заданный период при постоянных периодических выплатах и постоянной процентной ставке.

Синтаксис функции: PPMT(Ставка; Период; Кпер; Пс; Бс; Тип).

Задача 7. Составление графика погашения займа.

Взята ссуда размером 50 000р. на срок 2 года под 6% годовых с ежеквартальной выплатой платежей. Необходимо составить график погашения займа, включающий платежи по процентам и основные платежи..

Ход решения задачи.

1. При отсутствии исходного файла на листе ПЛТ дополните таблицу согласно таблице 12.

Таблица 12

Квартал	Платежи по процентам	Платежи по основной сумме	Платежи за период
1
2
3
4
5
6
7
8
Итого

2. Вычислите величину платежа по процентам для 1-го квартала.

3. Предусмотрев абсолютные ссылки, скопируйте формулу в ячейки для значений платежей по процентам остальных кварталов.

4. Вычислите величину основного платежа для 1-го квартала, используя необходимые значения из условия задачи 6.

5. Предусмотрев абсолютные ссылки, скопируйте формулу в ячейки для значений основных платежей остальных кварталов.

6. Определите итоговые величины платежей, суммировав платежи по процентам и основные платежи. Обратите внимание, что платежи должны быть одинаковыми для всех кварталов и равны значению периодического платежа задачи 6.

7. Вычислите итоговые значения всех видов платежей.

8. Результаты сравните с рисунком.

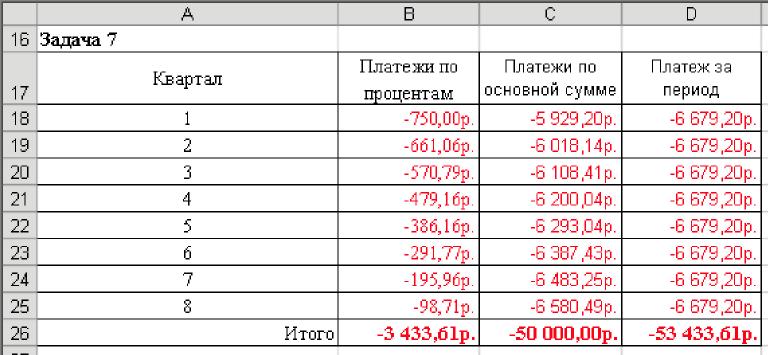
Рис. 5

9. Сохраните файл.

1.5. Расчет накоплений выплат по займу. Функции CUMIPMT (ОБЩПЛАТ), CUMPRINC(ОБЩДОХОД)

Функция CUMIPMT возвращает накопленный доход по займу между двумя перио­дами выплат. Эта функция будет доступной, если подключить надстройку Пакет анализа, выполнив команду Сервис^Надстройки.

Синтаксис функции:

CUMIPMT (Ставка; Кол_пер; Нз; Нач период; Кон _ период; Тип).

Аргумент Нач период - это номер первого периода, участвующего в вычислениях. Периоды нумеруются _ начиная с 1.

Аргумент Кон период служит для того, чтобы задать номер последнего периода, уча­ствующего в вычислениях.

Функция CUMIPMT очень близка по смыслу функции IPMT. Если функция IPMT вычисляет плату по процентам за отдельный период, то функция CUMIPMT может вычислить плату по процентам как за отдельный период, так и за несколько периодов.

Функция CUMPRINC возвращает основные выплаты по займу между двумя периодами. Эта функция будет доступной, если подключить надстройку Пакет анализа, выполнив команду Сервис⇒Надстройки.

Синтаксис функции:

CUMPRINC(Ставка; Кол_пер; Нз; Нач_период; Кон_период; Тип).

Аргумент Нач_период – это номер первого периода, участвующего в вычислениях. Периоды нумеруются, начиная с 1.

Аргумент Кон_период служит для того, чтобы задать номер последнего периода, участвующего в вычислениях.

Функция CUMPRINC можно назвать расширением функции PPMT. Функция PPMT вычисляет основные платежи в конкретный период. Результатом функции CUMPRINC может быть размер основных платежей как за конкретный период, так и за несколько периодов.

Задача 8. Составление графика погашения займа.

Взята ссуда размером 50 000р. на срок 2 года под 6% годовых с ежеквартальной выплатой платежей. Необходимо составить график погашения займа, включающий платежи по процентам и основные платежи.

Ход решения задачи.

1. При отсутствии исходного файла на листе ПЛТ дополните таблицу согласно таблицам 13-14.

Таблица 13

Выплаты по процентам
Основные выплаты
Общая сумма выплат

Таблица 14

Квартал	Накопление по процентам	Накопление по основной сумме	Остаток долга
1
2
3
4
5
6
7
8

2. Вычислите величину выплаты по процентам с помощью функции CUMIPMT, используя необходимые значения из условия задачи 6 и указав в качестве начального и конечного периодов соответственно 1 и 8 квартал.

3. Аналогичным образом вычислите величину выплаты по основной сумме с помощью функции CUMPRINC.

4. Определите общую сумму выплат, суммировав величины выплат по процентам и по основной сумме.

5. Результаты сравните с рисунком.

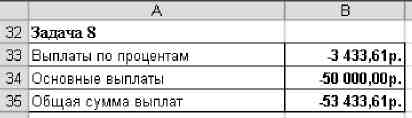
Рис. 6

6. Определите величину накопления по процентам для 1-го квартала, используя необходимые значения из условия задачи 6.

7. Предусмотрев абсолютные ссылки, скопируйте формулу в ячейки для значений накоплений по процентам остальных кварталов.

8. Результаты сравните с рисунком.

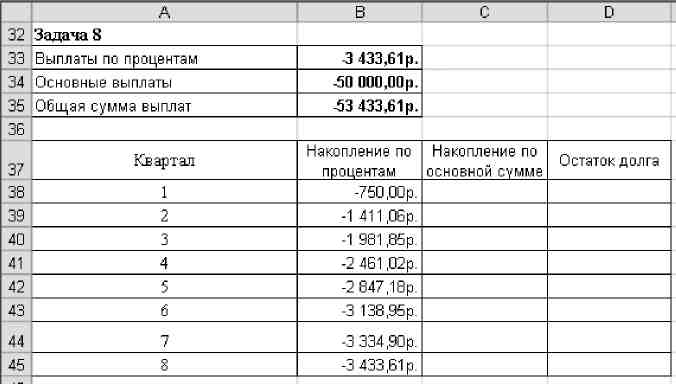
Рис. 7

9. Вычислите величину накопления по основной сумме для 1-го квартала, используя необходимые значения из условия задачи 6.

10. Предусмотрев абсолютные ссылки, скопируйте формулу в ячейки для значений накоплений по основной сумме остальных кварталов.

11. Результаты сравните с рисунком.

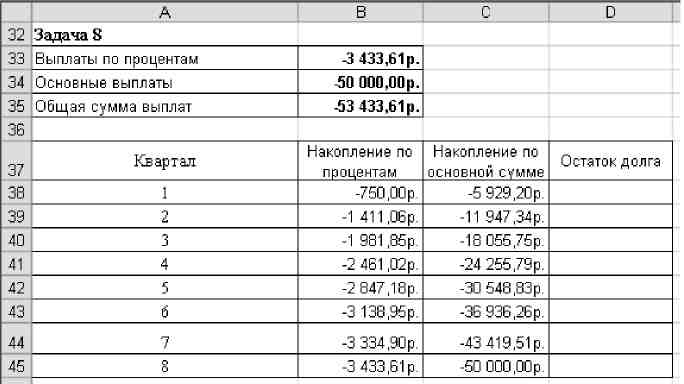
Рис. 8

12. Определите остаток долга, как разницу между суммой займа и накоплением по основной сумме.

13. Результаты сравните с рисунком.

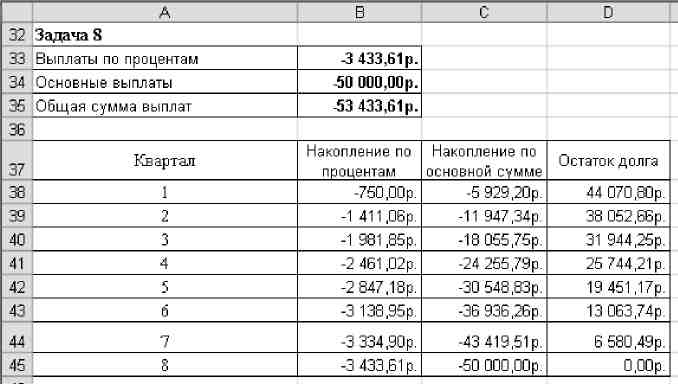
Рис 9

14. Сохраните файл

Задача 9. Расчет платежей по займу.

Рассчитайте размер ежегодной выплаты для погашения ссуды размером 220 000р., взятой на 7 лет под 9% годовых.

Определите основные платежи, платежи по процентам, остаток долга после очередной выплаты, общие суммы платежей по процентам, по основной сумме, платежей за период.

Ход решения задачи.

1. При отсутствии исходного файла на листе ПЛТ создайте таблицу согласно таблицам 15-17.

Таблица 15

Условия займа
Сумма займа	220 000,00р.
Процентная ставка годовая	9,0%
Срок займа в годах	7
Величина платежа

Таблица 16

График погашения займа
Квартал	Платежи по процентам	Платежи по основной сумме	Платеж за период	Накопление по основной сумме	Остаток долга
1
2
3
4
5
6
7
Итого

Таблица 17

Выплаты по процентам
Основные выплаты
Общая сумма выплат

2. Вычислите необходимые значения в соответствии с условием задачи.

3. Сохраните файл.

1.8. Расчет общего числа периодов выплат инвестиции. Функция NPER (КПЕР)

Функция NPER вычисляет, сколько периодов необходимо для погашения ссуды при заданной величине периодических выплат.

Синтаксис функции: NPER(Ставка; Плт; Пс; Бс; Тип).

Задача 10. Расчет срока ссуды.

В какой срок будет погашен долг в размере 100 000р., взятых под 8% годовых, если выплачивать ежемесячно по 1 000р.? Определите сумму комиссионных и общую сумму выплат по долгу.

Ход решения задачи.

1. При отсутствии исходного файла вставьте новый лист, назовите его NPER, создайте на листе таблицу согласно таблице 18.

Таблица 18

Сумма, взятая в долг	100 000,00р.
Выплата за период	-1 000,00р.
Периодичность выплат, раз/год	12
Годовая ставка	8,00%
Ставка за период
Количество периодов выплат
Срок инвестиции, лет
Сумма основных выплат
Сумма выплат по процентам
Общая сумма выплат

2. Вычислите количество периодов выплат с помощью функции NPER.

3. Определите срок инвестиции, разделив количество выплат на их периодичность.

4. Результаты сравните с рисунком.

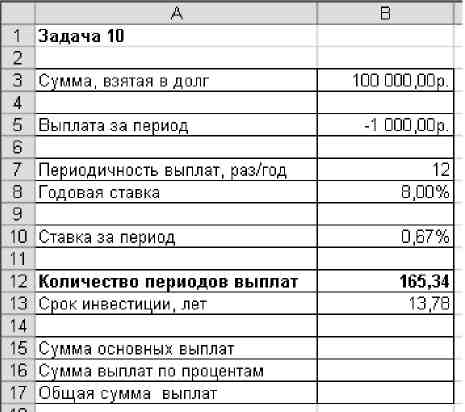
Рис 10

5. Вычислите сумму основных выплат, сумму выплат по процентам и общую сумму выплат.

6. Результаты сравните с рисунком.

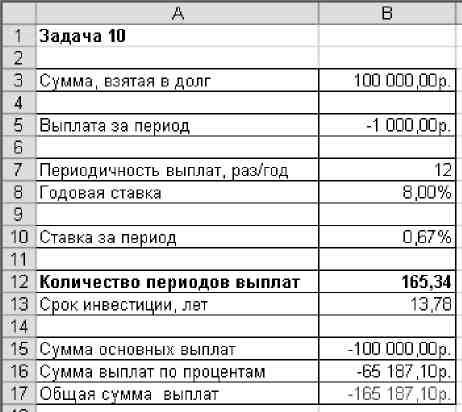
Рис 11

7. Сохраните файл.

Задача 11. Расчет срока займа.

Вы берете в долг 320 000р. Под 4,5% годовых и собираетесь выплачивать по 36 000р. в год. Сколько лет займут выплаты? Определить размер комиссионных и сумму выплат по займу.

Ход решения задачи.

1. При отсутствии исходного файла на листе NPER создайте таблицу согласно таблице 19.

Таблица 19

Сумма, взятая в долг	320 000,00р.
Выплата за период	-36 000,00р.
Периодичность выплат, раз/год	2
Годовая ставка	4,50%
Ставка за период
Количество периодов выплат
Срок инвестиции, лет
Сумма основных выплат
Сумма выплат по процентам
Общая сумма выплат

2. Вычислите необходимые значения в соответствии с условием задачи.

3. Сохраните файл.

1.9. Расчет нормы прибыли инвестиции. Функция RATE (СТАВКА)

Функция RATE позволяет определить скорость оборота (норму прибыли) вложения по ряду постоянных периодических выплат или/и по единовременной выплате. Другими словами, функция вычисляет процентную ставку за один период, необходимую для получения определенной суммы в течение заданного срока путем постоянных взносов.

Синтаксис функции: RATE(Кпер; Плт; Пс; Бс; Тип; Предположение).

Аргумент Плт (выплата) используется при определении скорости оборота для ряда постоянных периодических выплат, аргумент Бс (будущая стоимость) – при определении скорости оборота для единовременной выплаты.

Аргумент Предположение (по умолчанию равен 10%) дает начальное приближение нормы, т.к. OpenOffice.org Calc использует итерационный процесс для вычисления.

Задача 12. Определение годовой скорости оборота.

Организация сделала займ в размере $8000 на 4 года. Платежи должны производиться каждый месяц в размере $200. Определите, под какой процент взят займ. Учтите, что будущее значение инвестиции для займа составляет 0.

Ход решения задачи.

1. При отсутствии исходного файла вставьте новый лист, назовите его СТАВКА, создайте на листе таблицу согласно таблице 20.

Таблица 20

Сумма займа	$8 000,00
Объем платежей	-$200,00
Срок займа, лет	4
Периодичность выплат раз/год	12
Общее число периодов выплаты
Ставка за период
Годовая ставка

2. Вычислите ставку за период.

3. Определите годовую ставку, умножив ставку за период на периодичность платежей.

4. Результаты сравните с рисунком.

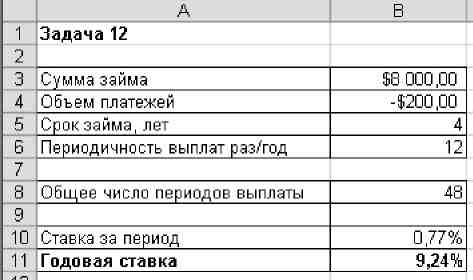
Рис 12

5. Сохраните файл.

Задача 13. Определение годовой ставки единовременной выплаты.

Рассматривается вложение сроком на 5 лет, которое гарантирует получение 5 000р. Сумма вложения составляет 3 000р. Определите годовую скорость оборота этого вложения.

Ход решения задачи.

1. При отсутствии исходного файла на листе СТАВКА создайте таблицу согласно таблице 21.

2. Вычислите годовую ставку.

3. Сохраните файл.

1.10. Определение модифицированной скорости оборота. Функция MIRR (МВСД)

Функция MIRR вычисляет модифицированную скорость оборота. Функция принимает во внимание стоимость занимаемых средств для финансирования инвестиции и предполагает, что средства, поступающие от этого вложения, можно реинвестировать. Функция считает, что все выплаты производятся в конце периодов, и возвращает эквивалентную процентную ставку за один период.

Синтаксис функции: MIRR(Значения; Ставка_финанс; Ставка_реинвест).

Аргумент Значения это массив платежей и поступлений, производимых в регулярные периоды времени.

Аргумент Ставка_финанс – это процентная ставка, по которой одалживаются средства, необходимые для вложения.

Аргумент Ставка_реинвест – это ставка, по которой реинвестируются средства, поступающие от вложения.

Задача 14. Определение модифицированной скорости оборота.

Рассматривается вложение сроком на 5 лет, которое гарантирует получение 5 000р. Сумма вложения составляет 3 000р.

Определите годовую скорость оборота этого вложения.

Ход решения задачи.

1. При отсутствии исходного файла на листе СТАВКА создайте таблицу согласно таблице 22.

2. Вычислите модифицированную ставку.

3. Сохраните файл.